

It is a little known fact that any particular colour of a rainbow, represented by a single wavelength in the electromagnetic spectrum, cannot be accurately represented using any three-colour process, whether this is RGB (Red, Green, Blue) as seen on computer monitors and TVs, or CMYK (Cyan, Magenta, Yellow (and blacK!)) as used in printing. Every colour to be displayed must lie within the "gamut", as it is called, of the primary colours of the system being used. Every single wavelength colour of the rainbow lies outside the possible range of any system. The best that can be achieved is a compromise of some sort.
For a good explanation of why this is so, together with a discussion about how to achieve rainbow colours on screen, visit:
http://aty.sdsu.edu/explain/optics/rendering.html
Also worth reading is:
https://en.wikipedia.org/wiki/CIE_1931_color_space
Once the number of colours required is known, one for each coloured square across the Braiding Rainbows window, a wavelength is assigned to each square, and the chromaticity calculated for each one. The subject of colour is a complex one, but chromaticity, put very simply, is a way of expressing the response of the eye to a colour in colour terms alone, without reference to how light or dark it might be. In addition, the response of the eye's cone cells for each primary colour is expressed as a percentage of the total of all three, which means that only two values are needed as the third can be easily worked out. Those two values allow chromaticity values to be plotted on a simple two-dimensional graph. This is the famous "horseshoe" colour diagram:
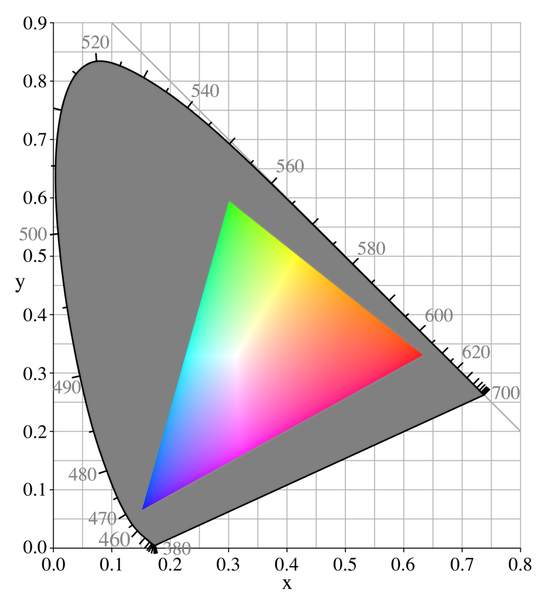
CIE 1931 xy Chromaticity Diagram - sRGB Primaries
In the diagram above, the coloured triangle represents the colours that are possible on an RGB monitor. The curved line round the outside of the "horseshoe" connects colours represented by a single wavelength, in other words all the colours of the rainbow. The grey area contains all the colours that cannot be displayed accurately on an RGB monitor. Famously, the colour of bluebells lies in this "out of gamut" area, as do many other colours found in nature.
Translating the chromaticity of true spectrum colours directly to a computer screen would result in negative values of Red, Green, or Blue, and that is obviously impossible. It is well known that mixing equal amounts of R, G, and B results in varying shades of grey between black and white (the chromaticity being the same in all cases), so a technique was developed of adding white to each spectrum colour until all values of R,G, and B were able to be represented by the RGB system, achieved by adjusting the chromaticity of the colour concerned in a straight line (straight on this two-dimensional diagram, that is) towards the white point of the system. This is not perfect, but yields reasonable results and is quick to calculate.
